অ-sinusoidal বর্তমান সঙ্গে বৈদ্যুতিক সার্কিট

অ-সাইনুসয়েডাল স্রোত এবং তাদের পচন

একটি বৈদ্যুতিক সার্কিটে, অ-সাইনোসয়েডাল স্রোত দুটি কারণে ঘটতে পারে:

1. বৈদ্যুতিক সার্কিট নিজেই রৈখিক, কিন্তু একটি নন-সাইনুসয়েডাল ভোল্টেজ সার্কিটে কাজ করে,

2. সার্কিটে যে ভোল্টেজ কাজ করে তা সাইনোসয়েডাল, কিন্তু বৈদ্যুতিক সার্কিটে অ-রৈখিক উপাদান থাকে।

উভয় কারণ থাকতে পারে। এই অধ্যায়টি শুধুমাত্র প্রথম পয়েন্টের জন্য সার্কিট নিয়ে আলোচনা করে। এই ক্ষেত্রে, অ-sinusoidal ভোল্টেজ পর্যায়ক্রমিক বলে মনে করা হয়।

পর্যায়ক্রমিক ডালের জেনারেটরগুলি রেডিও ইঞ্জিনিয়ারিং, অটোমেশন, টেলিমেকানিক্সের বিভিন্ন ডিভাইসে ব্যবহৃত হয়। ডালের আকৃতি ভিন্ন হতে পারে: করাত, ধাপযুক্ত, আয়তক্ষেত্রাকার (চিত্র 1)।

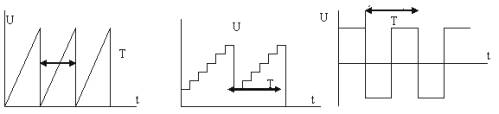
চিত্র 1. পালস আকার

ত্রিকোণমিতিক ফুরিয়ার সিরিজে ভোল্টেজ বক্ররেখা প্রসারিত হলে পর্যায়ক্রমিক কিন্তু নন-সাইনুসয়েডাল ভোল্টেজের অধীনে একটি রৈখিক বৈদ্যুতিক সার্কিটে ঘটে যাওয়া ঘটনাগুলি অধ্যয়ন করা সবচেয়ে সহজ:

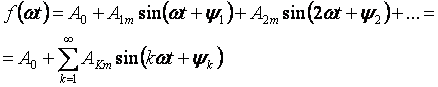
A0 সিরিজের প্রথম পদটিকে ধ্রুবক উপাদান বা জিরোথ হারমোনিক বলা হয়, সিরিজের দ্বিতীয় পদটি

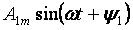
— মৌলিক বা প্রথম সুরেলা এবং ফর্মের অন্যান্য সকল সদস্য

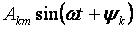
k> 1 এর জন্য উচ্চতর হারমোনিক্স বলা হয়।

যদি অভিব্যক্তিতে (3.1) আমরা যোগফলের সাইন খুলি, তাহলে আমরা সিরিজ লেখার অন্য ফর্মে যেতে পারি:

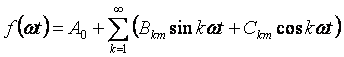যদি ফাংশনটি অ্যাবসিসা অক্ষ সম্পর্কে প্রতিসম হয়, তবে সিরিজটিতে একটি ধ্রুবক উপাদান থাকে না। যদি ফাংশনটি অর্ডিনেট অক্ষ সম্পর্কে প্রতিসম হয়, তাহলে সিরিজটিতে কোন সাইন থাকবে না। ফাংশনটি উৎপত্তি সম্পর্কে প্রতিসম এবং এতে কোন কোসাইন নেই।

সিরিজ সম্প্রসারণের কিছু উদাহরণ একটি টেবিলে দেওয়া হয়েছে। 1 এবং এগুলি রেফারেন্স সাহিত্যেও পাওয়া যায়।

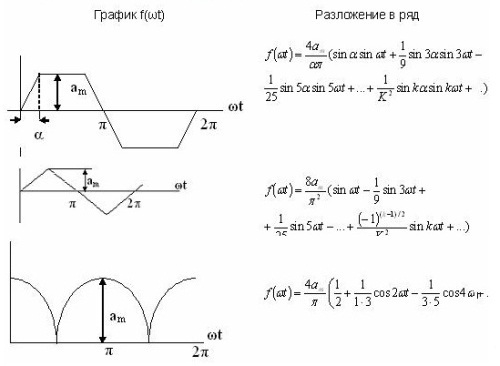
সারণী 1. ফুরিয়ার সিরিজ সম্প্রসারণ

অ-sinusoidal বর্তমান সার্কিট গণনা

মডেল অনুযায়ী প্রতিটি সুরেলা জন্য সার্কিট গণনা করা হয়। সার্কিটে যতবার ভোল্টেজ কাজ করে তাতে হারমোনিক্স থাকে ততবার সার্কিট গণনা করা হয়। এই ক্ষেত্রে, বেশ কয়েকটি বৈশিষ্ট্য বিবেচনায় নেওয়া প্রয়োজন।

এটি লক্ষ করা উচিত যে হারমোনিক সংখ্যা বৃদ্ধির সাথে সাথে প্রবর্তক উপাদানের প্রতিরোধ ক্ষমতা বৃদ্ধি পায়

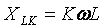
এবং ক্যাপাসিটিভ উপাদান, বিপরীতে, হ্রাস পায়:

এটিও বিবেচনায় নেওয়া উচিত যে কারেন্টের ধ্রুবক উপাদানটি ক্যাপাসিটরের মধ্য দিয়ে যায় না এবং ইন্ডাকট্যান্স এটিকে প্রতিরোধ করে না।

উপরন্তু, একটি সম্ভাব্য অনুরণন ঘটনা ভুলে যাওয়া উচিত নয় শুধুমাত্র মৌলিক সুরেলা, কিন্তু উচ্চ হারমোনিক্স এ.

ভেক্টর ডায়াগ্রাম প্রতিটি সুরেলা জন্য আলাদাভাবে প্লট করা যেতে পারে।

সুপারপজিশনের নীতি অনুসারে, প্রতিটি শাখার কারেন্ট পৃথক পদের সমষ্টি (শূন্য, মৌলিক এবং উচ্চতর সুরেলা) নিয়ে গঠিত হতে পারে:

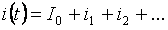
মোট শাখা প্রবাহের rms মান পৃথক সুরেলা স্রোতের গড় মান দ্বারা নির্ধারণ করা যেতে পারে:

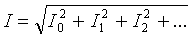
নন-সাইনোসয়েডাল কারেন্টের সক্রিয় শক্তি পৃথক হারমোনিক্সের সক্রিয় শক্তির সমষ্টির সমান:

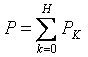
নীচে নন-সাইনুসয়েডাল কারেন্ট সার্কিট গণনা করার জন্য একটি সাধারণ উদাহরণ। সমস্ত স্রোত, ভোল্টেজ, প্রতিরোধের দুটি সূচক থাকবে: প্রথম সংখ্যাটি শাখা সংখ্যা এবং দ্বিতীয় সংখ্যাটি হারমোনিক সংখ্যা। ইনপুট ভোল্টেজ:

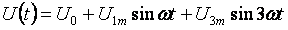
• স্থায়ী উপাদান

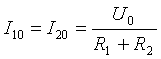
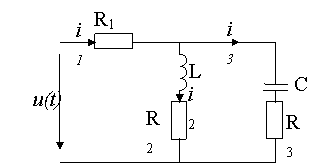
চিত্র 2. বৈদ্যুতিক চিত্র

• প্রধান হারমোনিক:

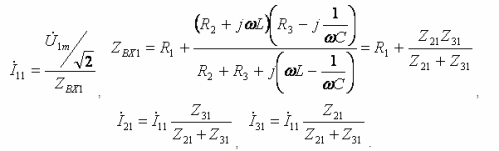
• তৃতীয় সুরেলা:

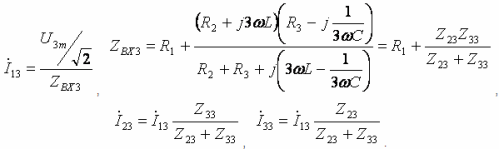
আরও পড়ুন: সবচেয়ে সাধারণ এসি থেকে ডিসি সংশোধন স্কিম