ক্রমাগত দোলন এবং প্যারামেট্রিক অনুরণন

ক্রমাগত কম্পন - কম্পন যার শক্তি সময়ের সাথে পরিবর্তিত হয় না। বাস্তব ভৌত ব্যবস্থায়, সর্বদা এমন কিছু কারণ থাকে যা কম্পন শক্তিকে তাপ শক্তিতে রূপান্তরিত করে (যেমন যান্ত্রিক সিস্টেমে ঘর্ষণ, বৈদ্যুতিক সিস্টেমে সক্রিয় প্রতিরোধ)।

অতএব, এই শক্তির ক্ষয়গুলি পুনরায় পূরণ করা হলেই কেবলমাত্র আবদ্ধ দোলনগুলি পাওয়া যেতে পারে। বাহ্যিক উত্স থেকে শক্তির কারণে স্ব-দোলক সিস্টেমে এই ধরনের পুনরায় পূরণ স্বয়ংক্রিয়ভাবে ঘটে। ক্রমাগত ইলেক্ট্রোম্যাগনেটিক দোলন অত্যন্ত ব্যাপকভাবে ব্যবহৃত হয়। সেগুলি পেতে বিভিন্ন জেনারেটর ব্যবহার করা হয়।

বৈদ্যুতিক বা যান্ত্রিক কম্পনগুলি (একটি দোলক বৃত্ত বা পেন্ডুলামের) নিরবচ্ছিন্ন করার জন্য, প্রতিরোধ বা ঘর্ষণজনিত ক্ষতির জন্য সর্বদা ক্ষতিপূরণ করা প্রয়োজন।

উদাহরণস্বরূপ, আপনি একটি বিকল্প ইএমএফের সাথে দোলক সার্কিটে কাজ করতে পারেন, যা পর্যায়ক্রমে কয়েলে কারেন্ট বাড়াবে এবং সেই অনুযায়ী, ক্যাপাসিটরে ভোল্টেজের প্রশস্ততা বজায় রাখবে।অথবা আপনি দুলটিকে একইভাবে ধাক্কা দিতে পারেন, এটি সুরেলাভাবে দুলতে থাকে।

আপনি জানেন যে, দোলক সার্কিটের কুণ্ডলীর চৌম্বক ক্ষেত্রের শক্তির মাত্রা নিম্নোক্ত সম্পর্কের দ্বারা এর আবেশ এবং প্রবাহের সাথে সম্পর্কিত (দ্বিতীয় সূত্রটি হলক্যাপাসিটরের বৈদ্যুতিক ক্ষেত্রের শক্তি একই কনট্যুর কনট্যুর)

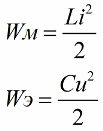
প্রথম সূত্র থেকে এটা স্পষ্ট যে আমরা যদি পর্যায়ক্রমে কুণ্ডলীতে কারেন্ট বাড়াই, বিকল্প EMF সার্কিটে কাজ করে, তাহলে (সূত্রের দ্বিতীয় ফ্যাক্টর — কারেন্ট বাড়িয়ে বা হ্রাস করে) আমরা পর্যায়ক্রমে এই সার্কিটটিকে শক্তি দিয়ে পুনরায় পূরণ করব।

বর্তনীতে তার প্রাকৃতিক মুক্ত দোলনগুলির সাথে সময়মতো কঠোরভাবে কাজ করা, অর্থাৎ, অনুরণিত ফ্রিকোয়েন্সিতে, আমরা বৈদ্যুতিক অনুরণনের ঘটনাটি পাব, কারণ এটি অনুরণিত ফ্রিকোয়েন্সিতে রয়েছে দোদুল্যমান সিস্টেম সবচেয়ে নিবিড়ভাবে এটিতে সরবরাহ করা শক্তি শোষণ করে।

কিন্তু যদি আপনি পর্যায়ক্রমে দ্বিতীয় ফ্যাক্টর (কারেন্ট বা ভোল্টেজ নয়) পরিবর্তন করেন তবে প্রথম ফ্যাক্টর - ইনডাক্ট্যান্স বা ক্যাপাসিট্যান্স পরিবর্তন করেন? এই ক্ষেত্রে, সার্কিটটি তার শক্তিতেও পরিবর্তন আনবে।

উদাহরণস্বরূপ, পর্যায়ক্রমে কয়েলের ভিতরে এবং বাইরে কোরকে ধাক্কা দেওয়া বা ক্যাপাসিটরের ভিতরে এবং বাইরে ঠেলে দেওয়াঅস্তরক, — আমরা সার্কিটের শক্তিতে একটি খুব নির্দিষ্ট পর্যায়ক্রমিক পরিবর্তনও পাই।

কয়েল ইনডাক্টেন্সে ইউনিট পরিবর্তনের জন্য আমরা এই অবস্থানটি লিখি:

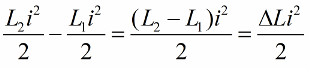
সার্কিটের সুইং এর সবচেয়ে স্পষ্ট প্রভাব হবে যদি ইনডাক্টেন্স পরিবর্তন ঠিক সময়ে করা হয়। উদাহরণ স্বরূপ, আমরা যদি একই সার্কিটটি সময়ের যেকোনো মুহূর্তে গ্রহণ করি, যখন কিছু কারেন্ট i ইতিমধ্যেই এর মধ্য দিয়ে প্রবাহিত হয় এবং কয়েলে একটি কোর প্রবর্তন করি, তাহলে শক্তি নিম্নলিখিত পরিমাণে পরিবর্তিত হবে:

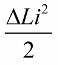
এখন বর্তনীতেই মুক্ত দোলন দেখা যাক, কিন্তু এই মুহুর্তে যখন, এক চতুর্থাংশ সময় পরে, শক্তি সম্পূর্ণরূপে ক্যাপাসিটরের মধ্যে চলে যায় এবং কয়েলে কারেন্ট শূন্য হয়ে যায়, তখন আমরা হঠাৎ করে কয়েল থেকে কোরটি সরিয়ে ফেলব ইনডাক্ট্যান্স। প্রারম্ভিক মান L-এ তার আসল অবস্থায় ফিরে আসবে। কোরটি সরানো হলে চৌম্বক ক্ষেত্রের বিরুদ্ধে কোন কাজ করার প্রয়োজন নেই। অতএব, যখন কোরটি কয়েলে ঠেলে দেওয়া হয়েছিল, তখন সার্কিট শক্তি পেয়েছিল, যেহেতু আমরা কাজ করেছি, যার মান:

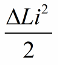
পিরিয়ডের এক চতুর্থাংশ পরে, ক্যাপাসিটরটি নিঃসৃত হতে শুরু করে, এর শক্তি আবার কয়েলের চৌম্বক ক্ষেত্রের শক্তিতে রূপান্তরিত হয়। যখন চৌম্বক ক্ষেত্র প্রশস্ততায় পৌঁছে, আমরা আবার কোরটিকে তীব্রভাবে চাপব। আবার ইন্ডাকট্যান্স বেড়েছে, একই পরিমাণ বেড়েছে।

এবং আবার, শূন্য কারেন্টে, আমরা ইন্ডাকট্যান্সকে তার আসল মান ফিরিয়ে দিই। ফলস্বরূপ, যদি প্রতিটি অর্ধ-চক্রের জন্য শক্তি লাভ প্রতিরোধের ক্ষতির চেয়ে বেশি হয়, তাহলে লুপের শক্তি সর্বদা বৃদ্ধি পাবে এবং দোলন প্রশস্ততা বৃদ্ধি পাবে। এই পরিস্থিতি অসমতা দ্বারা প্রকাশ করা হয়:

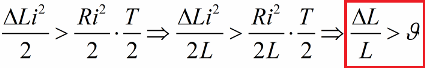
এখানে আমরা এই অসমতার উভয় দিককে L দ্বারা ভাগ করেছি এবং লগারিদমিক হ্রাসের একটি নির্দিষ্ট মানের জন্য লাফ দিয়ে প্যারামেট্রিক উত্তেজনার সম্ভাবনার শর্ত লিখেছি।

প্রতি পিরিয়ডে দুইবার ইন্ডাকট্যান্স (বা ক্যাপাসিট্যান্স) পরিবর্তন করার পরামর্শ দেওয়া হয়, তাই প্যারামিটার পরিবর্তনের ফ্রিকোয়েন্সি (প্যারামেট্রিক রেজোন্যান্স ফ্রিকোয়েন্সি) দোদুল্যমান সিস্টেমের স্বাভাবিক ফ্রিকোয়েন্সি দ্বিগুণ হওয়া উচিত:

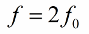
তাই সার্কিটে দোলনের উত্তেজনার পথটি সরাসরি ইএমএফ বা কারেন্ট পরিবর্তন করার প্রয়োজন ছাড়াই হাজির হয়েছে।সার্কিটে প্রাথমিক ওঠানামাকারী কারেন্ট সবসময়ই কোনো না কোনোভাবে উপস্থিত থাকে এবং এটি বায়ুমণ্ডলে রেডিও ফ্রিকোয়েন্সি দোলনের হস্তক্ষেপকেও বিবেচনা করে না।

যদি ইন্ডাকট্যান্স (বা ক্যাপাসিট্যান্স) জাম্পে পরিবর্তিত না হয়, কিন্তু সুরেলাভাবে, তাহলে দোলনের ঘটনার অবস্থা একটু ভিন্ন দেখাবে:

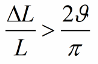
যেহেতু ক্যাপাসিট্যান্স এবং ইন্ডাকট্যান্স হল সার্কিট প্যারামিটার (যেমন একটি পেন্ডুলামের ভর বা একটি স্প্রিং এর স্থিতিস্থাপকতা), উত্তেজনাপূর্ণ দোলনের পদ্ধতিকে প্যারামেট্রিক উত্তেজনাও বলা হয়।

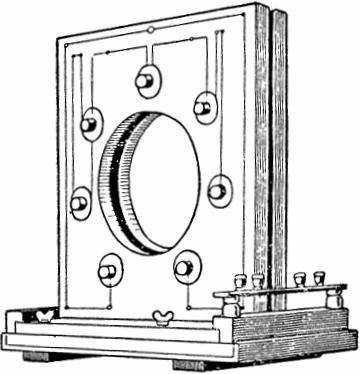
এই ঘটনাটি 20 শতকের শুরুতে সোভিয়েত পদার্থবিদ ম্যান্ডেলস্টাম এবং পাপালেক্সি দ্বারা আবিষ্কৃত এবং কার্যত অধ্যয়ন করা হয়েছিল। এই ভৌত ঘটনার উপর ভিত্তি করে, তারা 4 কিলোওয়াট শক্তি এবং পরিবর্তনশীল ইন্ডাকট্যান্স সহ প্রথম প্যারামেট্রিক এসি জেনারেটর তৈরি করেছিল।

জেনারেটরের ডিজাইনে, ফ্রেমের উভয় পাশে সাত জোড়া ফ্ল্যাট কয়েল ছিল, যার গহ্বরে প্রোট্রুশন সহ একটি ফেরোম্যাগনেটিক ডিস্ক ঘোরানো হয়েছিল। যখন ডিস্কটি মোটর দ্বারা ঘোরানোর জন্য চালিত হয়, তখন এর প্রোট্রুশনগুলি পর্যায়ক্রমে প্রতিটি কয়েলের মধ্যে স্থানের মধ্যে এবং বাইরে চলে যায়, যার ফলে আবেশ এবং উত্তেজনাপূর্ণ দোলনগুলি পরিবর্তন হয়।