সার্কিট টপোলজিস - মৌলিক ধারণা

একটি বৈদ্যুতিক সার্কিট হল ডিভাইস (উপাদান) এবং তাদের সংযোগকারী তারগুলির একটি সেট যার মাধ্যমে বৈদ্যুতিক প্রবাহ প্রবাহিত হতে পারে। বৈদ্যুতিক সার্কিট শেয়ার সব উপাদান নিষ্ক্রিয় এবং সক্রিয় মধ্যে.

সক্রিয় উপাদান বিভিন্ন ধরনের শক্তি (যান্ত্রিক, রাসায়নিক, আলো, ইত্যাদি) বৈদ্যুতিক শক্তিতে রূপান্তর করে। নিষ্ক্রিয় ডিভাইসগুলিতে, বৈদ্যুতিক শক্তি অন্য ধরণের শক্তিতে রূপান্তরিত হয়। সক্রিয় উপাদানগুলিকে উত্স বলা হয়, নিষ্ক্রিয় উপাদানগুলিকে ভোক্তা বা গ্রহণকারী বলা হয়।

সার্কিট তত্ত্বে, বৈদ্যুতিক উপাদানগুলির আদর্শ মডেল বিবেচনা করা হয়। এটি উপাদানগুলির বর্ণনাকে যতটা সম্ভব সহজ করে তোলে। আরও জটিল, বাস্তব উপাদানগুলি আদর্শ উপাদানগুলির একটি সেট থেকে তৈরি করা হয়।

বৈদ্যুতিক সার্কিটের প্রধান নিষ্ক্রিয় উপাদানগুলি হল প্রতিরোধক (প্রতিরোধী উপাদান), সূচনাকারী (ইন্ডাকটিভ উপাদান) এবং ক্যাপাসিটর (ক্যাপাসিটিভ উপাদান)। একটি প্রদত্ত মান এবং আকৃতির ভোল্টেজ এবং কারেন্ট তৈরি করতে উপাদানগুলি একটি বৈদ্যুতিক সার্কিটে ইনস্টল করা হয় (দেখুন — বৈদ্যুতিক সার্কিট এবং এর উপাদান).

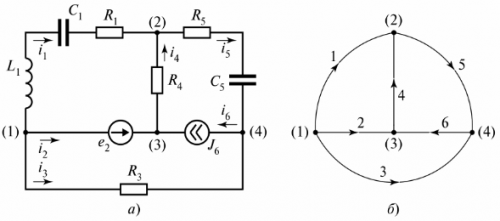
একটি বৈদ্যুতিক সার্কিট শাখা এবং নোড নিয়ে গঠিত। শাখা — এটি একটি বৈদ্যুতিক সার্কিটের (সার্কিট) একটি অংশ যার মধ্য দিয়ে একই কারেন্ট প্রবাহিত হয়। একটি গিঁট - তিন বা ততোধিক শাখার সংযোগ। বৈদ্যুতিক চিত্রে, নোডটি একটি বিন্দু দ্বারা নির্দেশিত হয় (চিত্র 1)।

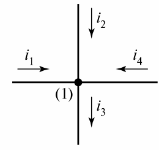
ভাত। 1. ডায়াগ্রামে নোডটি সংজ্ঞায়িত করুন

প্রয়োজনে, ডায়াগ্রামের নোডগুলি বাম থেকে ডানে উপরে থেকে নীচে পর্যন্ত সংখ্যাযুক্ত।

ডুমুরে। 2 রেজিস্টিভ-ক্যাপাসিটিভ শাখা দেখায় যেখানে বর্তমান আইসি প্রবাহিত হয়।

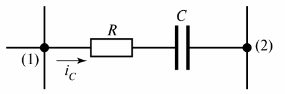
ভাত। 2. প্রতিরোধী-ক্যাপাসিটিভ শাখা

একটি শাখার আরেকটি সংজ্ঞা দেওয়া যেতে পারে - এটি দুটি সংলগ্ন নোডের (নোড (1) এবং (2) চিত্র 2-এর মধ্যে একটি সার্কিটের একটি বিভাগ)।

চেইন বৈদ্যুতিক সার্কিটে কোন বন্ধ পথ আছে কি? সার্কিট যে কোনো শাখা দ্বারা বন্ধ করা যেতে পারে, শর্তাধীন শাখা সহ যার প্রতিরোধ অসীম সমান।

ডুমুরে। 3 একটি শাখাযুক্ত বৈদ্যুতিক সার্কিট দেখায় যা তিনটি শাখা নিয়ে গঠিত।

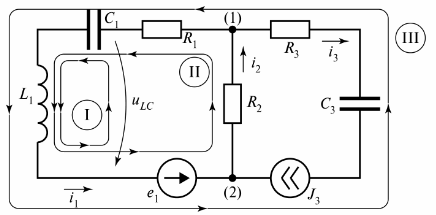
ভাত। 3. দুটি সার্কিট সহ বৈদ্যুতিক সার্কিট

চিত্রটি তিনটি সার্কিট দেখায়, এবং সার্কিট I অসীম প্রতিরোধের একটি শাখা দ্বারা বন্ধ করা হয়। এই শাখাটি ভোল্টেজ টিএলসি হিসাবে নির্দেশিত হয়।

চিত্রের সার্কিটের জন্য। 3 বাস্তব বা শর্তসাপেক্ষ শাখা দ্বারা বন্ধ করা অনেকগুলি লুপ রচনা করা সম্ভব, তবে বৈদ্যুতিক শব্দের গণনার জন্য "স্বাধীন লুপ" ধারণাটি ব্যবহৃত হয়। স্বাধীন সার্কিট লুপের সংখ্যা সর্বদা গণনার জন্য প্রয়োজনীয় সর্বনিম্ন হিসাবে সেট করা হয়।

স্বাধীন সার্কিট সবসময় বন্ধ থাকে, কিন্তু যে শাখাগুলির প্রতিরোধ ক্ষমতা অসীমের সমান নয়, এবং প্রতিটি স্বাধীন সার্কিটে অন্তত একটি শাখা থাকে যা অন্য সার্কিটে অন্তর্ভুক্ত নয়। জটিল বৈদ্যুতিক সার্কিটের জন্য, আপনি সার্কিট ডায়াগ্রাম ব্যবহার করে স্বাধীন সার্কিটের সংখ্যা নির্ধারণ করতে পারেন।

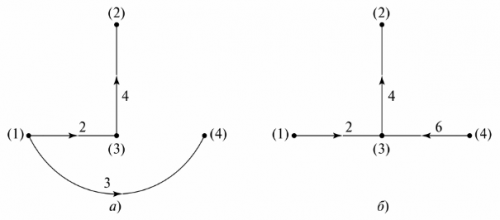
সার্কিট ডায়াগ্রামে সার্কিটের একটি শর্তসাপেক্ষ উপস্থাপনা বলা হয়, যেখানে প্রতিটি শাখা একটি লাইন সেগমেন্ট দ্বারা প্রতিস্থাপিত হয়। শাখায় আইটেম প্রদর্শিত হয় না. উদাহরণস্বরূপ, FIG. 4 একটি শাখা সার্কিট এবং এর ডায়াগ্রাম দেখায়।

ভাত। 4. শাখাযুক্ত বৈদ্যুতিক সার্কিট: a — সার্কিট ডায়াগ্রাম, b — ডায়াগ্রাম

একটি ডায়াগ্রামের একটি চিত্র তৈরি করতে, আপনাকে অবশ্যই নোডগুলিকে তাদের উপর উপাদানগুলি উল্লেখ না করে শাখা লাইনের সাথে সংযুক্ত করতে হবে। শাখাগুলি সংখ্যাযুক্ত, এবং তাদের উপর স্রোতের দিকগুলি তীর দ্বারা নির্দেশিত হয়। গ্রাফের নিজেই কোন শারীরিক অর্থ নেই, তবে স্বাধীন কনট্যুর সংখ্যা এবং প্রকার নির্ধারণ করতে ব্যবহার করা যেতে পারে। এই উদ্দেশ্যে, একটি "গ্রাফিক গাছ" প্রস্তুত করা হয়।

গ্রাফিক গাছ এটি এমন একটি সার্কিটের গ্রাফ উপস্থাপন করে যার নোডগুলি এমনভাবে শাখা দ্বারা সংযুক্ত থাকে যাতে কোনও বন্ধ লুপের ফলাফল হয় না। একটি গ্রাফিক্যাল ট্রি প্রদর্শনের জন্য বিভিন্ন বিকল্প থাকতে পারে। ডুমুরে। 5 FIG এর সার্কিটের জন্য দুটি সম্ভাব্য বিকল্প দেখায়। 4.

ভাত। 5. স্কিমের গ্রাফিক ট্রি

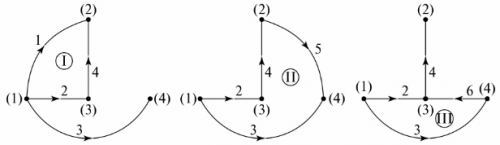
গ্রাফ ট্রিতে অনুপস্থিত শাখার সংখ্যা সার্কিটের স্বাধীন লুপের সংখ্যার সমান। উদাহরণে, এগুলি তিনটি শাখা, তিনটি স্বাধীন লুপ। স্বাধীন লুপগুলির কনফিগারেশন গ্রাফ ট্রির নোডগুলিকে গ্রাফ ট্রিতে নির্দিষ্ট করা নেই এমন শাখাগুলির সাথে ক্রমানুসারে সংযুক্ত করে প্রাপ্ত করা যেতে পারে। উদাহরণস্বরূপ, চিত্রে গ্রাফ ট্রির জন্য। 5, এবং স্বাধীন কনট্যুরগুলি ডুমুরে দেখানো হয়েছে। 6.

ভাত। 6. গ্রাফ ট্রির মাধ্যমে স্বাধীন কনট্যুর নির্ধারণ করা

সার্কিট গণনার জন্য স্বাধীন সার্কিট কনফিগার করার জন্য একটি বিকল্প নির্বাচন সার্কিট বিশ্লেষণের সময় বাহিত হয়। আপনার এই ধরনের কনট্যুরগুলি বেছে নেওয়া উচিত যাতে গণনা যতটা সম্ভব সহজ হয়, যেমন সিস্টেমে নির্ভরশীল সমীকরণের সংখ্যা ন্যূনতম।

টপোলজিকাল সমীকরণগুলি একটি সার্কিটে ভোল্টেজ এবং স্রোতের মধ্যে একটি সম্পর্ক স্থাপন করে এবং সমীকরণের সংখ্যা এবং প্রকার শাখাগুলিতে কোন উপাদানগুলি অন্তর্ভুক্ত রয়েছে তার উপর নির্ভর করে না। টপোলজিক্যাল সমীকরণগুলি গঠিত সমীকরণগুলিকে অন্তর্ভুক্ত করে Kirchhoff এর আইন অনুযায়ী.